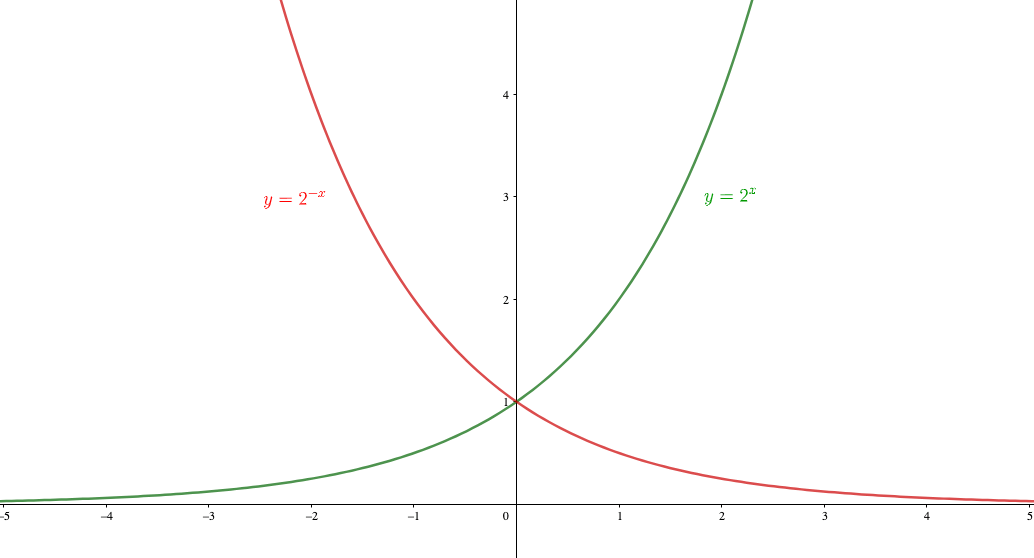
漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので,f(x)≒ax+b ・・・① とおける。両辺を x で割って,lim計算すると,lim( ) ( ) lim x b a x f x x x x漸近線を持つ代表的な関数 漸近線はない場合もありますし、複数ある場合もあります。 ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。 指数関数 \(y=2^x,y=2^{x}\)はグラフのようになりますが、\(x\)軸に着目すると漸近線である微分のやり方まとめ! お疲れ様でした! 数学Ⅱまでに学習する微分の計算は、とてもシンプルで簡単なものばかりでした。 一方、数学Ⅲに突入するとかなり難しくなる(^^;)
数 微分の範囲の問題で 漸近線についてわからないことがあります Yahoo 知恵袋
微分 グラフ 漸近線 求め方
微分 グラフ 漸近線 求め方-ー1) を通るから 0 apローー ig2ニータ うー の には) こ 2 お 関数 ゞニ logi(x寺4)十1 のグラフは 3 0) を通るから pmすすロニ0 6yGの =ュ (14x49)G パー12xt 21x ⑨の左辺を PC) と (9 はー2 を因数 7G9 をァー2 て割る デー10x ィー2)ゼエー12 一22 ー10x ー10 よって PGG) = @ょり Ge2(G 2 このなかで, *=2、5また、漸近線や接線の方程式、媒介変数表示なども説明していくので、ぜひこの記事を通してマスターしてくださいね! 楕円とは?方程式の書き方、面積・焦点・接線の求め方 接線、接線の方程式とは?公式や微分による傾きの求め方



数 標準問題精巧 高校数学に関する質問 勉強質問サイト
== 漸近線の方程式 == 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。漸近線の描き方を一目にまとめました。 漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください.★の数は優先度です.★→★★→★★★ の順に取り組みましょう.3332 30←→ ポイント集をまとめて見たい場合 点線
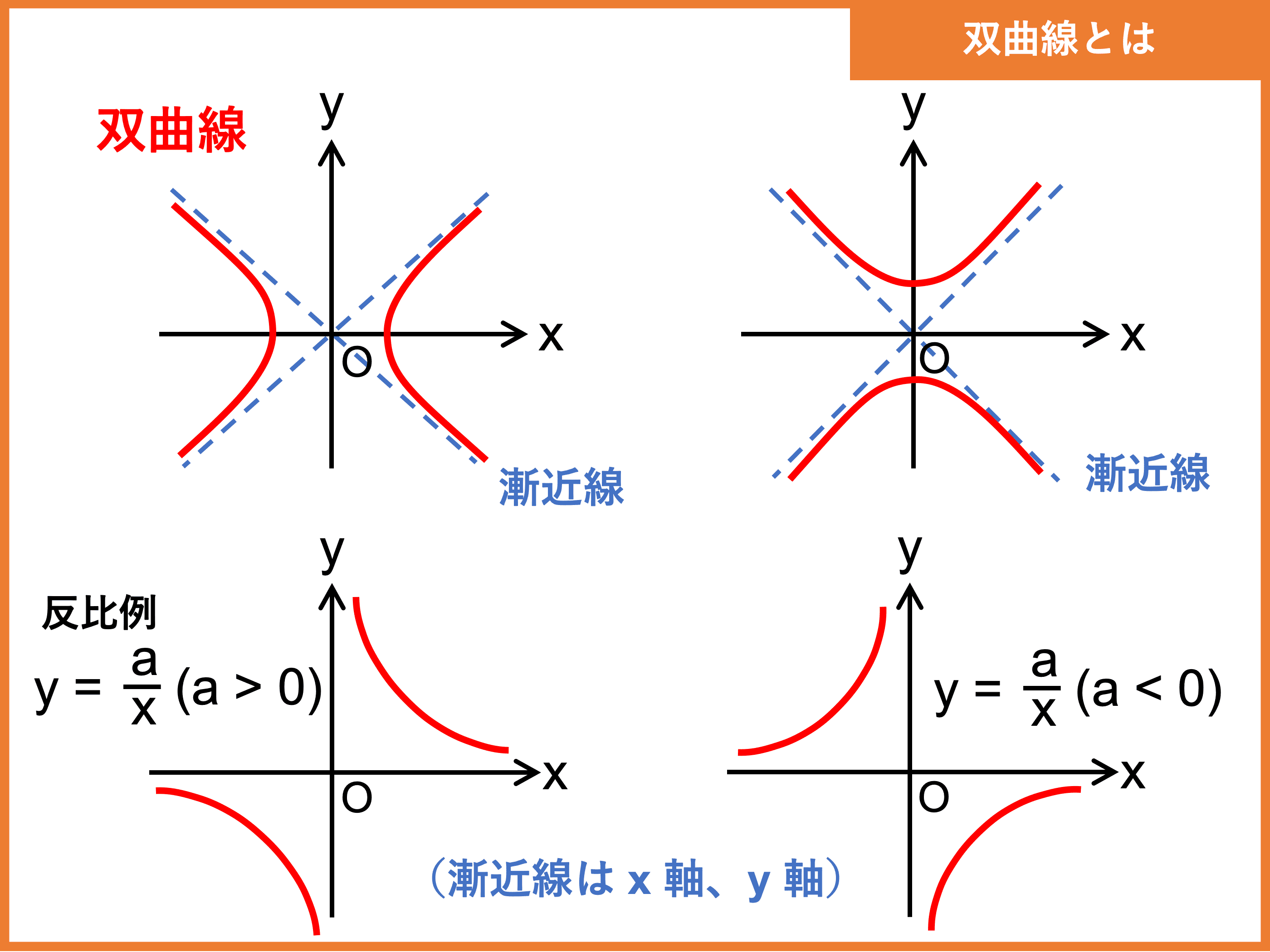
こんにちは、ウチダショウマです。 今日は、数学Ⅱで初めて登場するが詳しくは数学Ⅲで習う 「漸近線」 について、求め方、意味、定義について解説していきます! 主な具体例(分数関数や双曲線)も挙げながら詳しく見ていきましょう♪ 漸近線とは まずは聞き慣れない言葉だと思いますので漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) limこれを利用して右側微分と左側微分を求め,その値が異なる点を漸近線として判定します。 const Range = 18;
Sin^1(x/a)を微分しても、 1/√(a^2-x^2)にたどり着けません。 なんで漸近線を持つ直角双曲線がこのような形になるんですか?? この形は分数関数の形じゃないですか! 写真の図からxの標準偏差Sx、yの標準偏差Sy、xyの共分散Sxyの求め方を教えてー1) を通るから 0 apローー ig2ニータ うー の には) こ 2 お 関数 ゞニ logi(x寺4)十1 のグラフは 3 0) を通るから pmすすロニ0 6yGの =ュ (14x49)G パー12xt 21x ⑨の左辺を PC) と (9 はー2 を因数 7G9 をァー2 て割る デー10x ィー2)ゼエー12 一22 ー10x ー10 よって PGG) = @ょり Ge2(G 2 このなかで, *=2、5漸近線を持つ代表的な関数 漸近線はない場合もありますし、複数ある場合もあります。 ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。 指数関数 \(y=2^x,y=2^{x}\)はグラフのようになりますが、\(x\)軸に着目すると漸近線である



漸近線とは 求め方 高校数学 Youtube



微分法の応用 高校数学に関する質問 勉強質問サイト
いただいた nb を見て、漸近線の求め方の別解?も「2次曲線について4.」としてブログにあげさせてもらいました。ありがとうございます。 整数解の方は、Wolfram alpha に解かせたところ、無限個あるようですね。漸近線の描き方を一目にまとめました。 漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm> 微分法(iii)複雑な関数のグラフのかき方 もっと正確なグラフをかくことを要求された場合は, これに加えて, 変曲点や漸近線, グラフの対称性などを調べることで, より正確なグラフをかくことができます。 数列Σの和の求め方


微分法の応用のグラフの書き方について この解説の増減表まではかけるの Yahoo 知恵袋



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
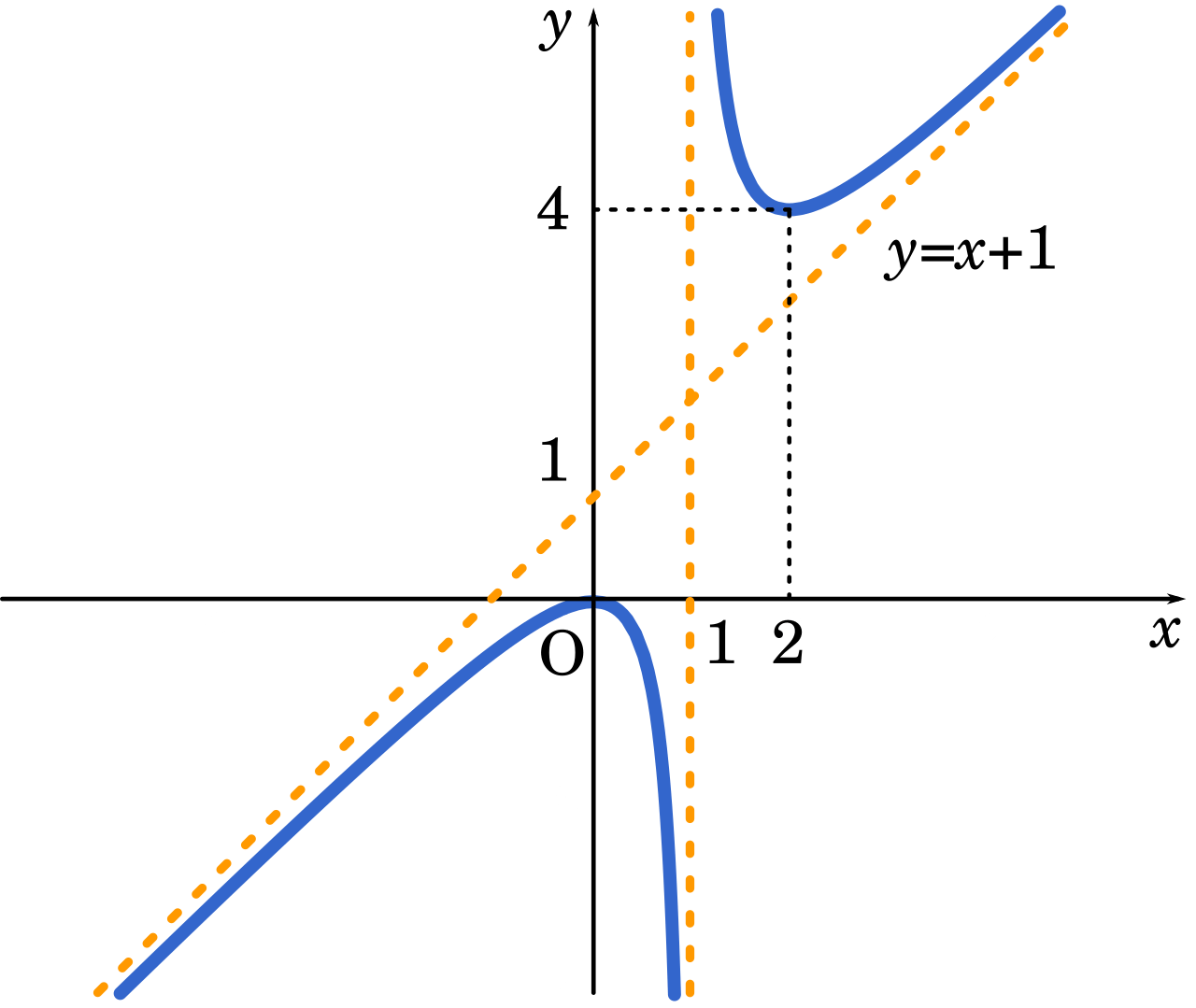
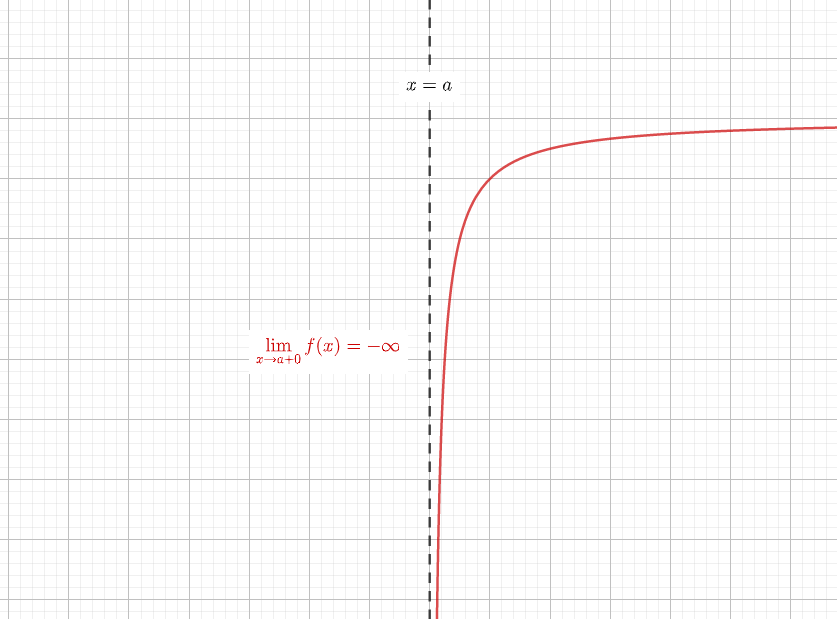
漸近線の一般的な求め方は次の通りです。 (1) x軸に垂直な漸近線の場合 lim f(x) (x→a+0の時)、lim f(x) (x→a-0の時)の内、少なくとも1つが+∞または-∞になれば、直線x=aが漸近線である。漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、漸近線の方程式 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。 したがって,漸近線の方程式を単独で問うことはまれです。



高校数学 1次分数関数の決定 受験の月
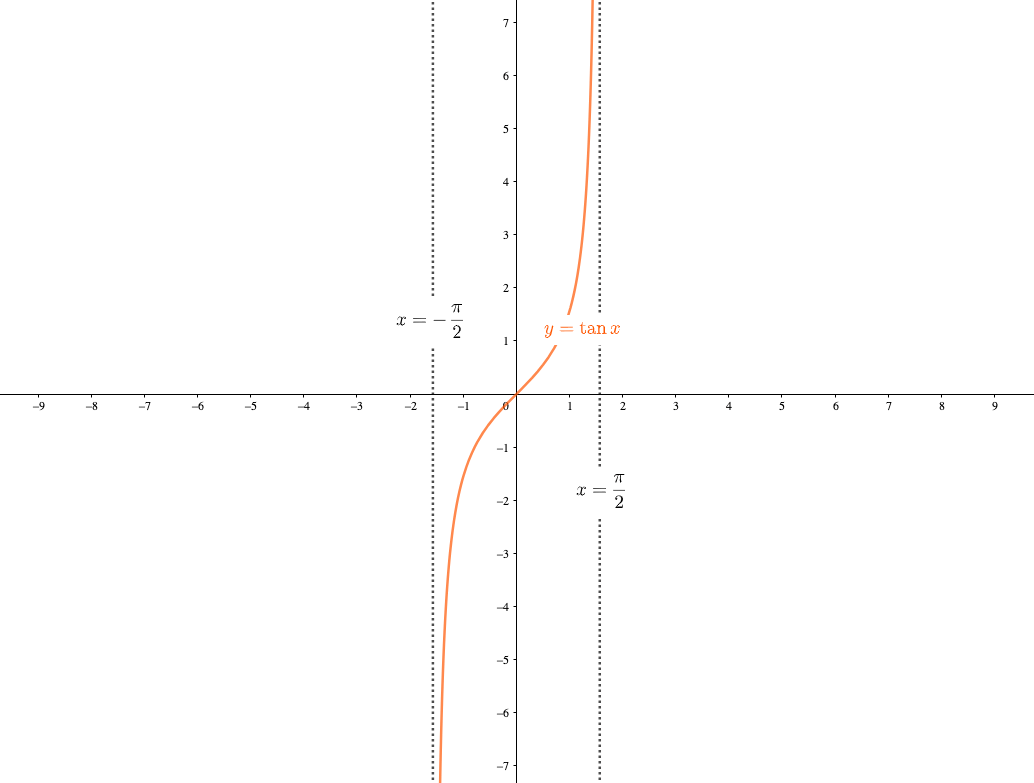


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
漸近線の一般的な求め方は次の通りです。 (1) x軸に垂直な漸近線の場合 lim f(x) (x→a+0の時)、lim f(x) (x→a-0の時)の内、少なくとも1つが+∞または-∞になれば、直線x=aが漸近線である。//始点のx座標 const h = range;> 微分法(iii)複雑な関数のグラフのかき方 もっと正確なグラフをかくことを要求された場合は, これに加えて, 変曲点や漸近線, グラフの対称性などを調べることで, より正確なグラフをかくことができます。 数列Σの和の求め方
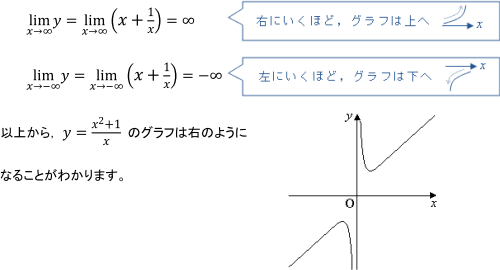


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座
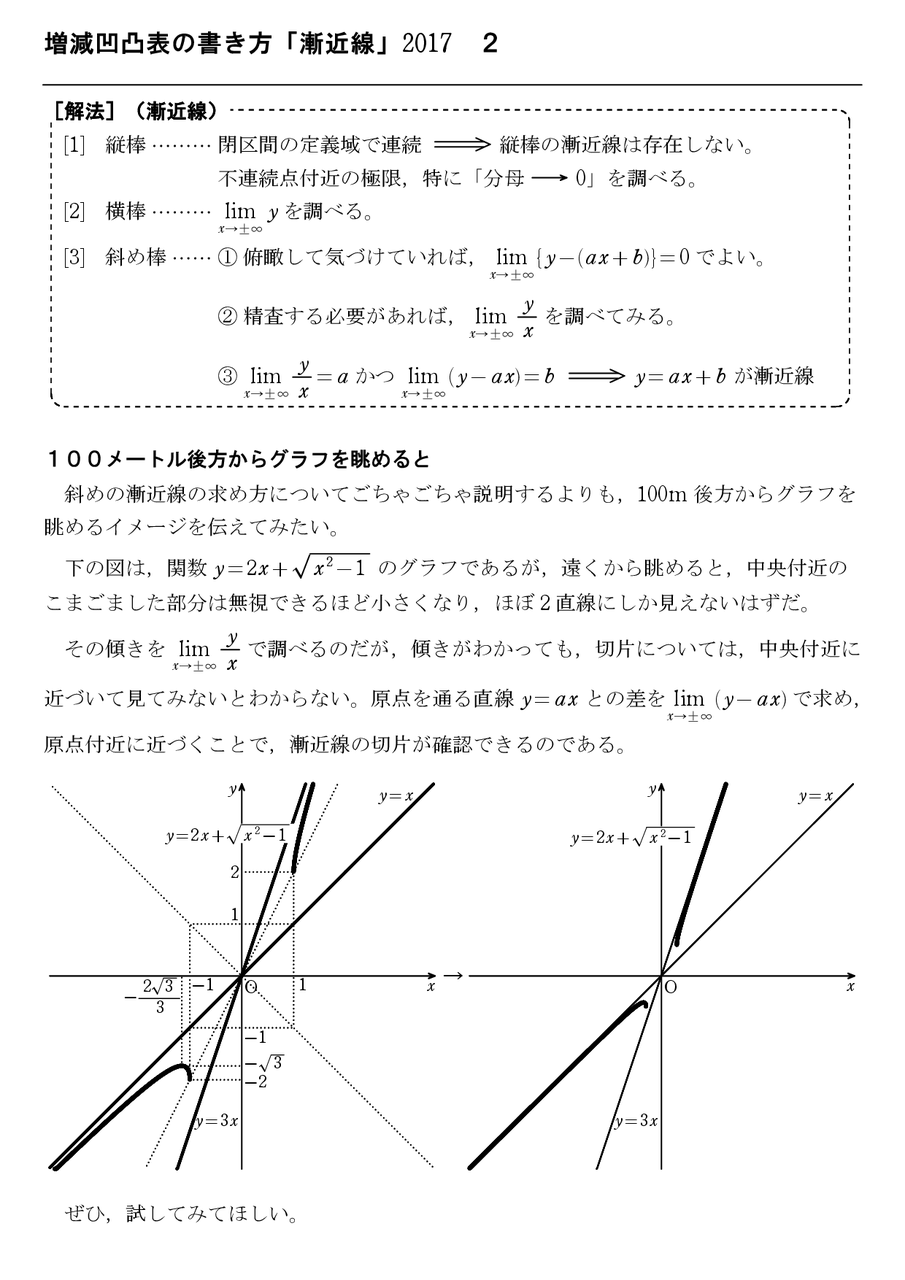


増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する
漸近線とは「しだいに近づいていく直線」のことです。 「しだいに近づいていく」をもう少しきちんと言うと「十分遠くで距離が限りなく $0$ に近づいていく」です。この説明でだけでは漸近線の意味が分かりにくいので、3つの具体的な漸近線のパターンを双曲線の漸近線について,具体例,簡単な導出方法,きちんとした証明を解説します。 例題 漸近線とは,関数が 原点から遠い部分で限りなく近づく直線 のことです。 まずは具体例から。// x軸両端の幅 const range = Range / 400;



漸近線の求めかた Y X 1 1 X 1 のグラフを描く問題なんですが 数学 教えて Goo
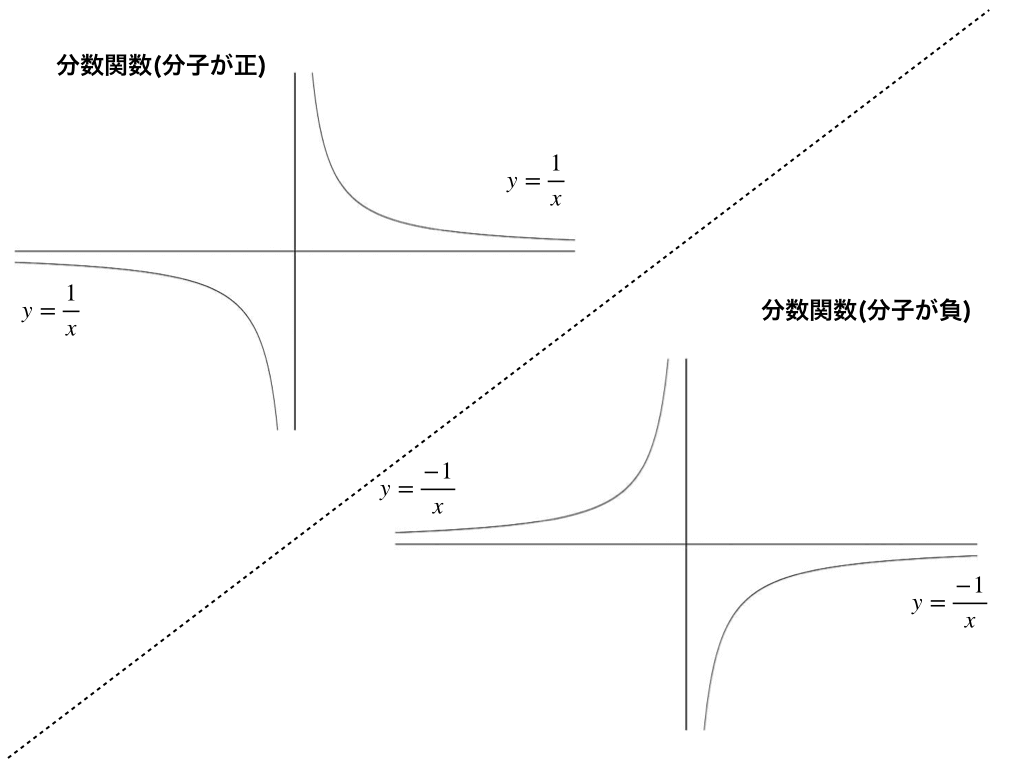


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法
Let x = Range / 2;



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
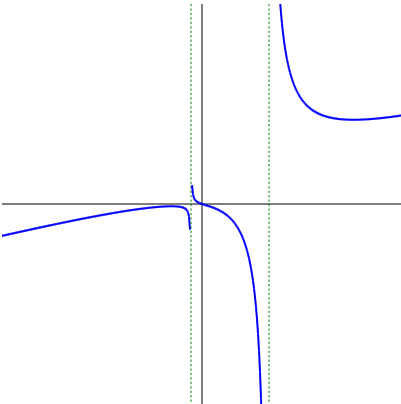


Javascript Y軸に平行な漸近線を描く Mm参考書
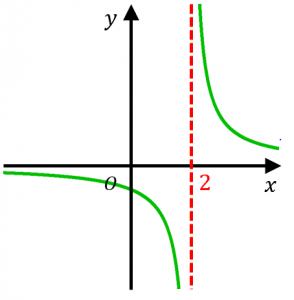


漸近線の求め方3パターン 具体例で学ぶ数学



漸近線を調べて 概形をかけ という問題です 漸近線を求めると 高校数学に関する質問 勉強質問サイト



高校数学 漸近線の求め方 前編 増減表で自動化 タテ ヨコ 予想法 Youtube



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



数3 関数の極限 グラフ 漸近線 高校数学に関する質問 勉強質問サイト
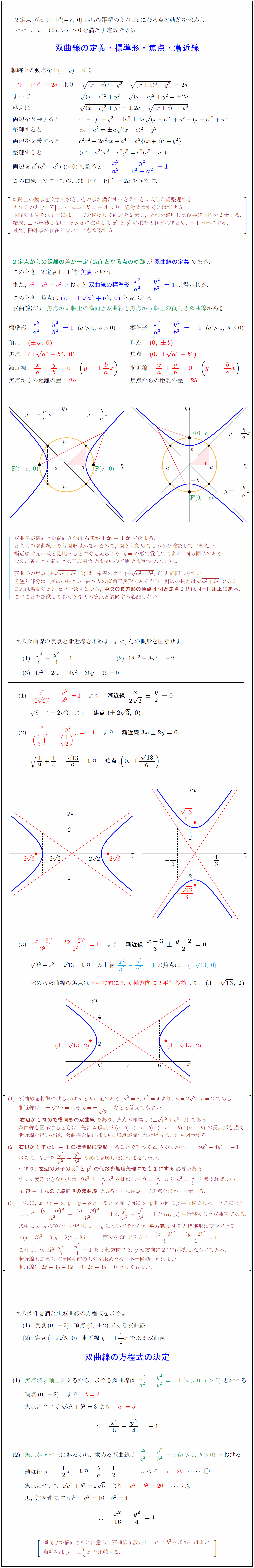


高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月
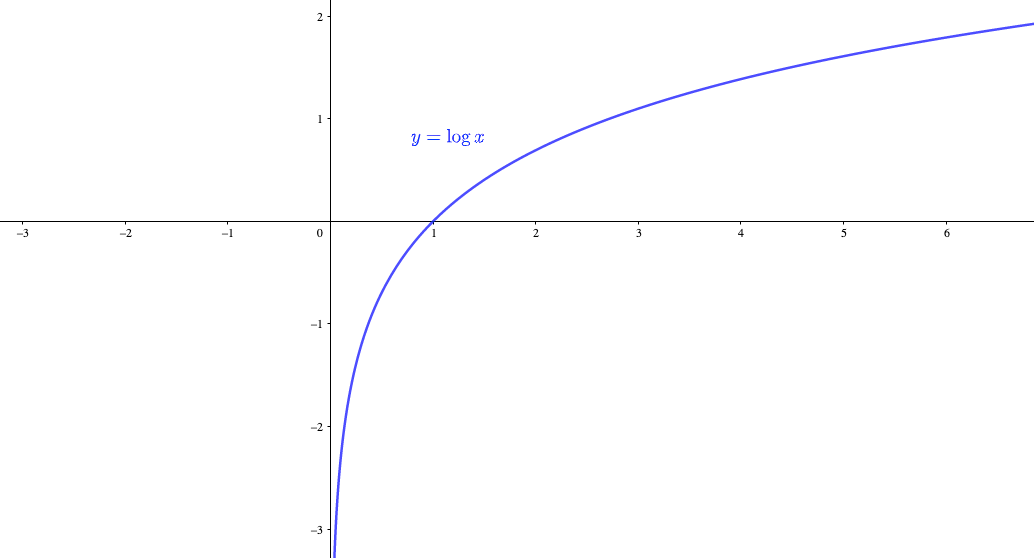


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
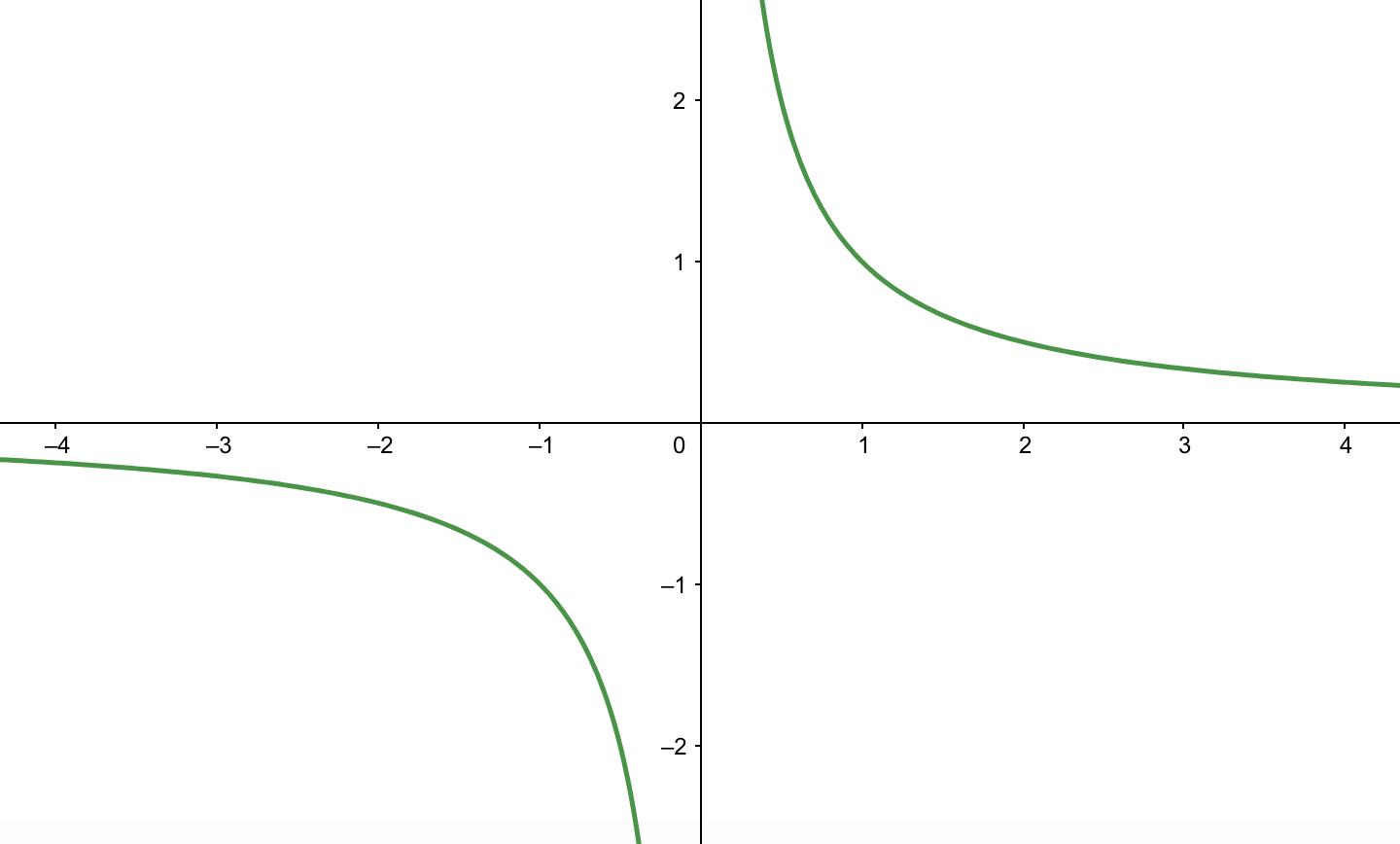


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット



漸近線公式 雙曲線 漸近線の求め方 導出方法あり 5分でわかる Krgez


双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典


漸近線の方程式


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線 点線じゃなきゃ ダメですか 実線だったら バツなんですか Clear


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clear



数3微分のグラフについてです この問題の漸近線の求め方が分かりません Clear


高校数学の数3の漸近線の求め方なのですが なぜ括弧の中のような事 Yahoo 知恵袋


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット


漸近線の方程式
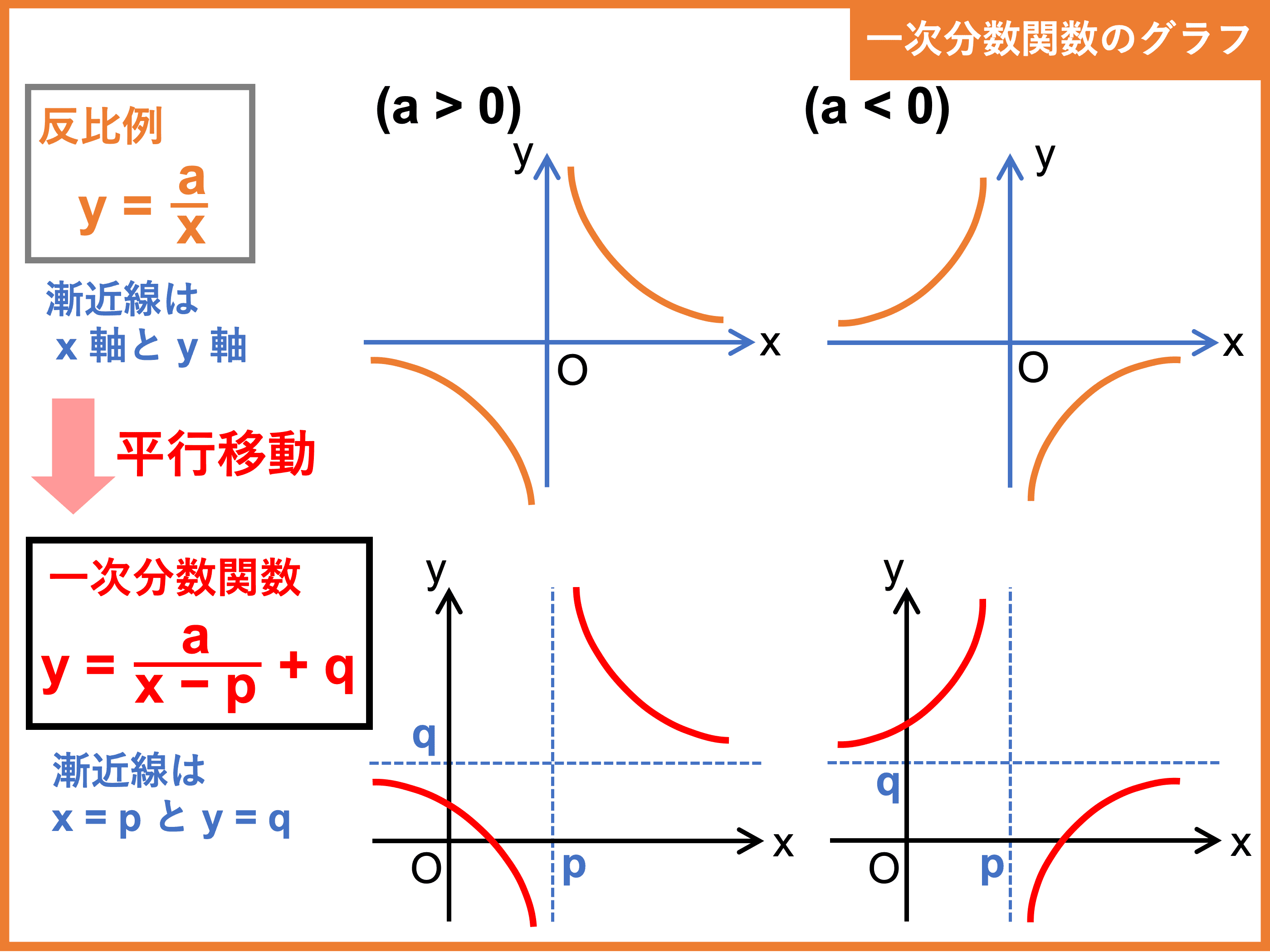


分数関数とは グラフや微分 積分 不等式の解き方 受験辞典



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



のx軸に平行な漸近線でlim X F X になった 高校数学に関する質問 勉強質問サイト
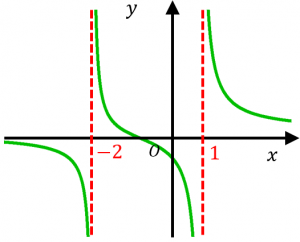


漸近線の求め方3パターン 具体例で学ぶ数学



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



高校数学 双曲線の接線と漸近線に関する有名性質 受験の月


関数の漸近線を求める方法なんですけど したの画像のように式変形しないと Yahoo 知恵袋



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


どうして 中心が原点 漸近線の傾きが 2で 点 1 2 0 を通 Yahoo 知恵袋



漸近 線 求め 方 Article



漸近線を調べて 概形をかけ という問題です 漸近線を求めると 高校数学に関する質問 勉強質問サイト
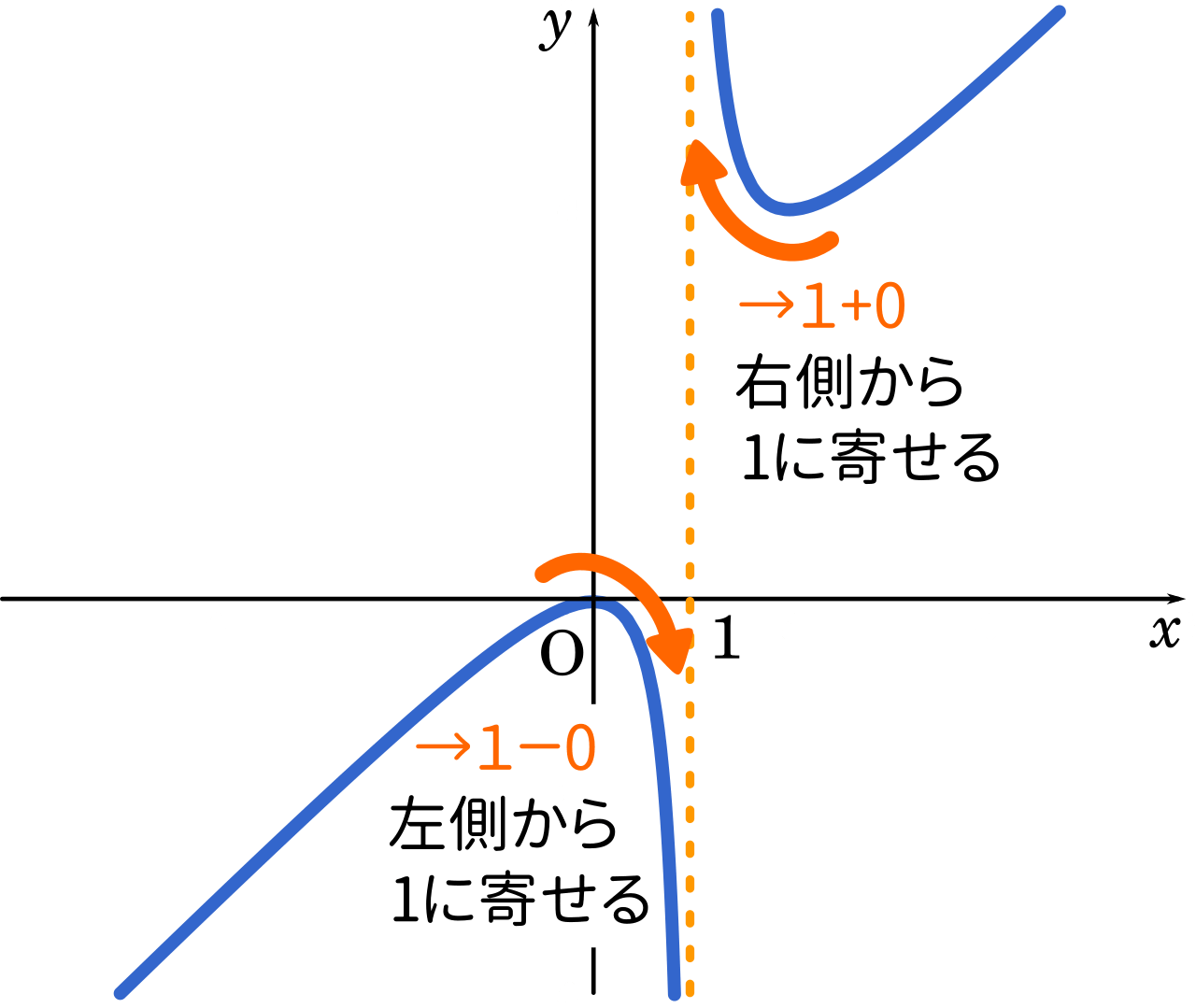


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す


数 微分の範囲の問題で 漸近線についてわからないことがあります Yahoo 知恵袋



数 標準問題精巧 高校数学に関する質問 勉強質問サイト



基礎から学ぶ 数学iii 曲線の漸近線 Youtube



高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月



三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
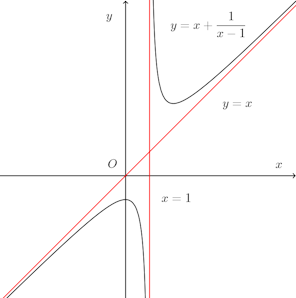


ねこ騙し数学
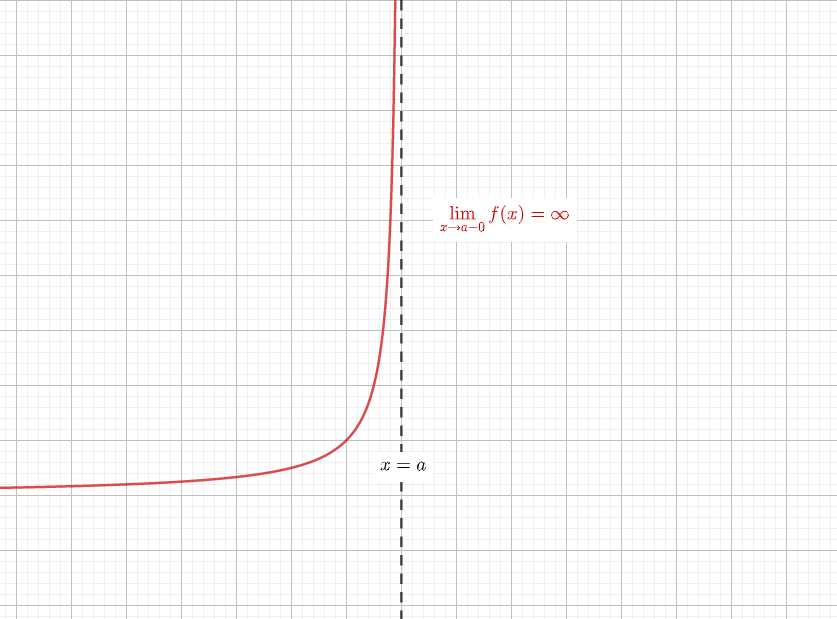


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


漸近線についての質問です 微分のグラフを書くときの漸近線の求め方が分かり Yahoo 知恵袋



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法
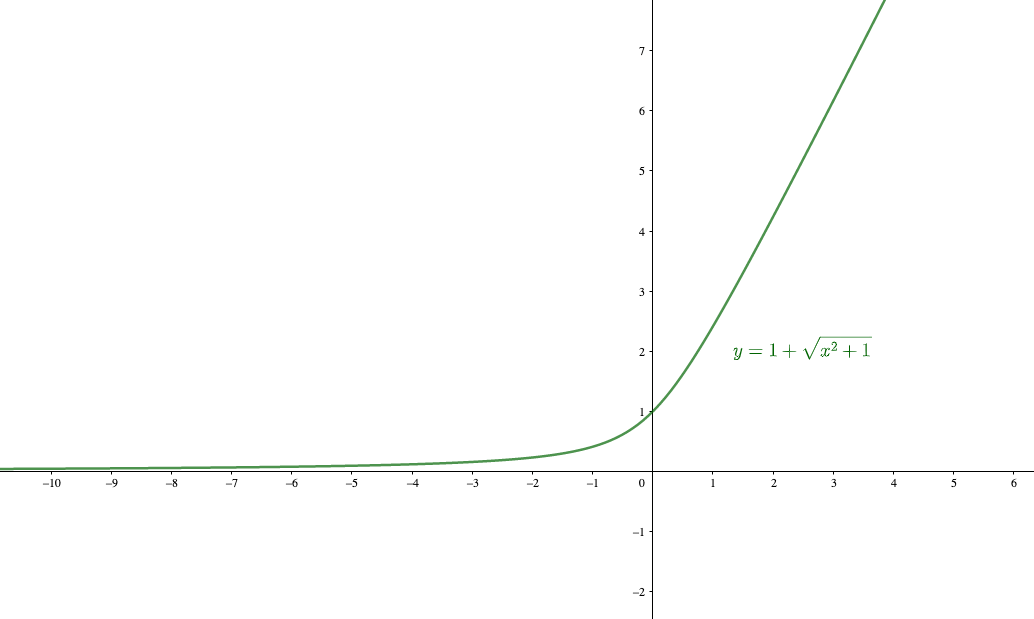


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
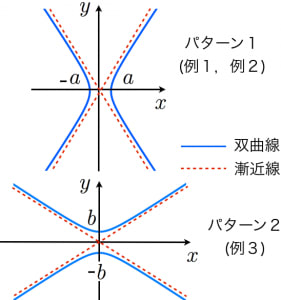


双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語



対数関数の漸近線の求め方がわかりません ス せ ソの解説をお願いしたいです Clear
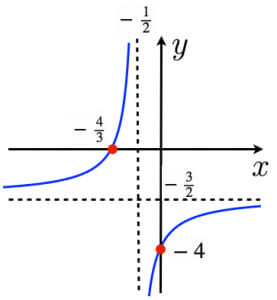


一次分数関数のグラフと漸近線 高校数学の美しい物語
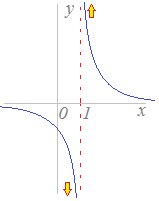


漸近線の方程式



数3 関数の極限 グラフ 漸近線 高校数学に関する質問 勉強質問サイト



対数関数の漸近線の求め方がわかりません ス せ ソの解説をお願いしたいです Clear
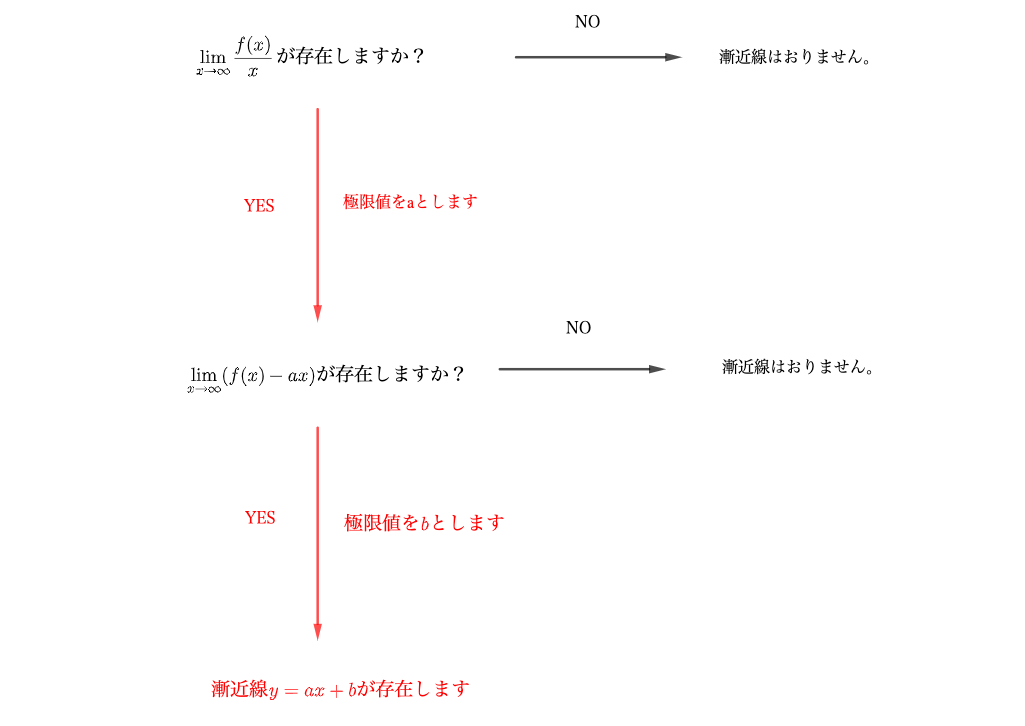


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す



高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット



漸近線の求め方 高校数学 微分法の応用 14 Youtube
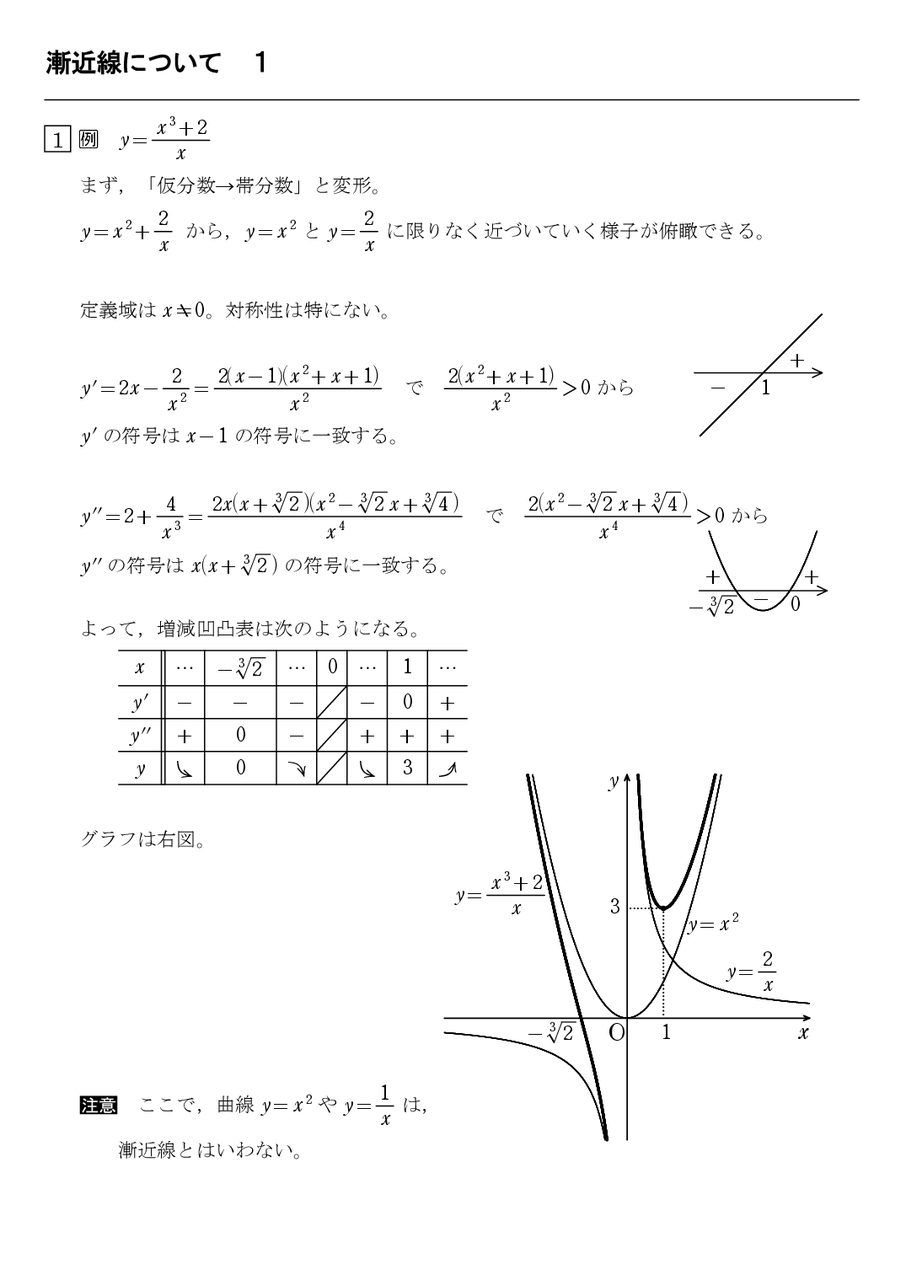


増減凹凸表を書く手順 7 漸近線 1 怜悧玲瓏 高校数学を天空から俯瞰する
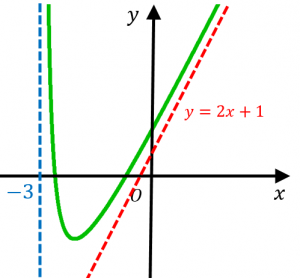


漸近線の求め方3パターン 具体例で学ぶ数学



漸近線の求め方 高校数学 微分法の応用 14 Youtube



大学入試数学 M1 19 09 漸近線 求め方 導関数 Derivative 微分 Differential 微分法differentiation Youtube


漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋


数学の青チャートの問題です 写真の漸近線の求め方について 解説の定義域ではこの Yahoo 知恵袋



数3の微分の応用のところの漸近線の求め方がわかりません Clear
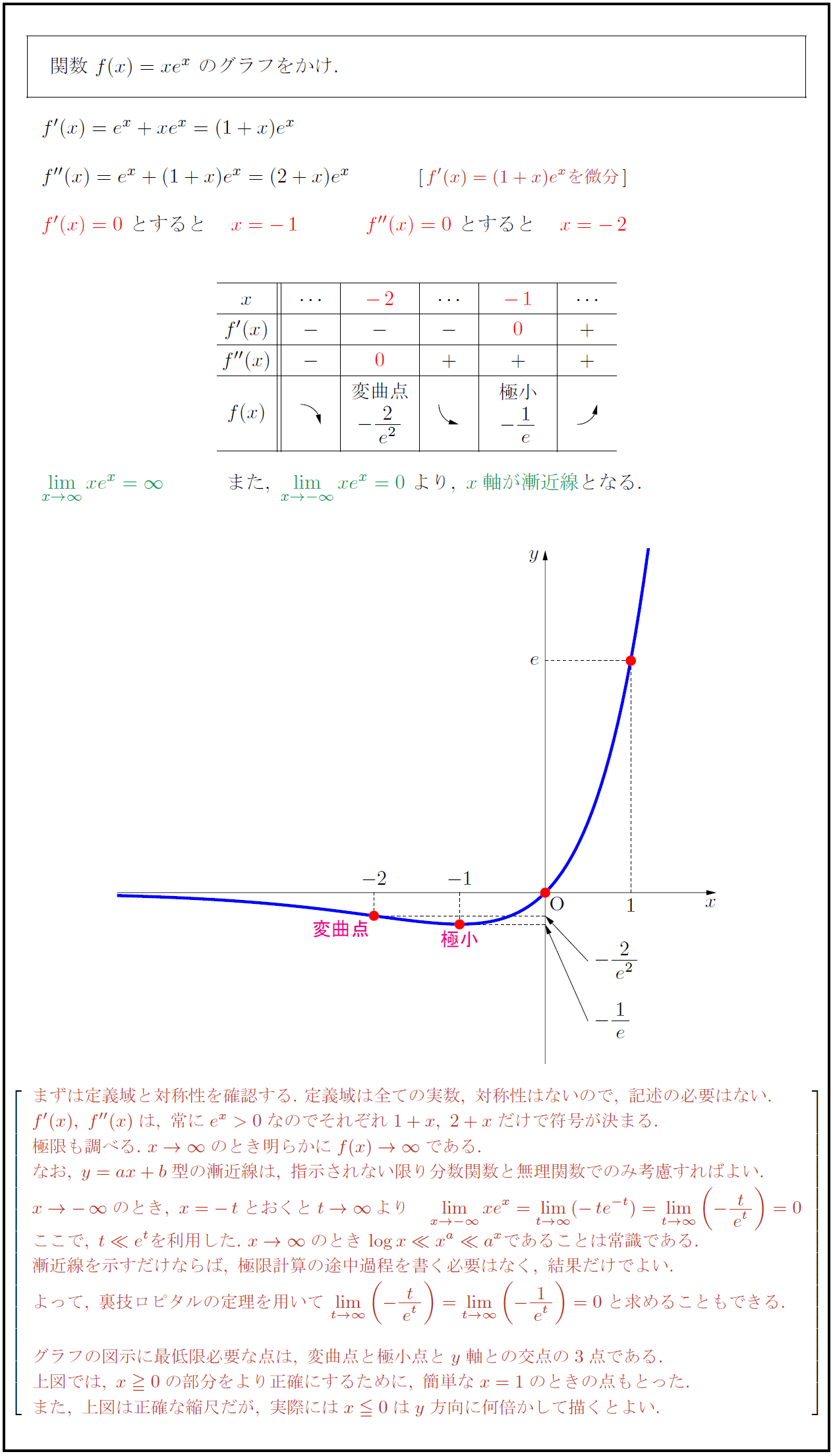


高校数学 指数関数 Y Xe X のグラフ 受験の月
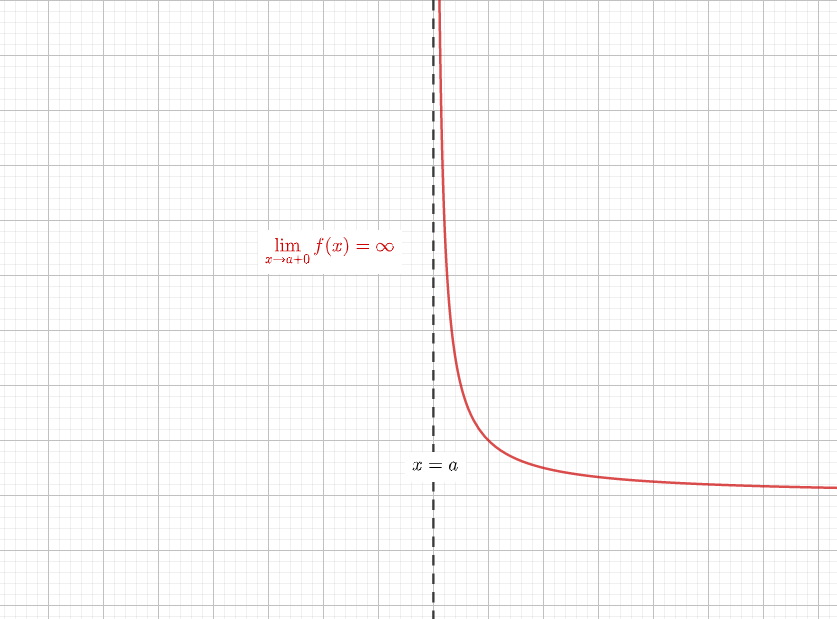


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



Y Tan8のグラフの漸近線の求め方を教えて下さい 1 はわかったのですが 2 Clear


数3グラフの概形を書くときに漸近線を調べると思うんですが どこを調べれば Yahoo 知恵袋



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
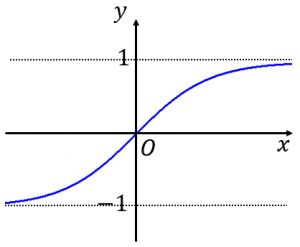


Tanhの意味 グラフ 微分 積分 具体例で学ぶ数学



数学3です なぜy Xが漸近線だといえるのでしょうか Clear
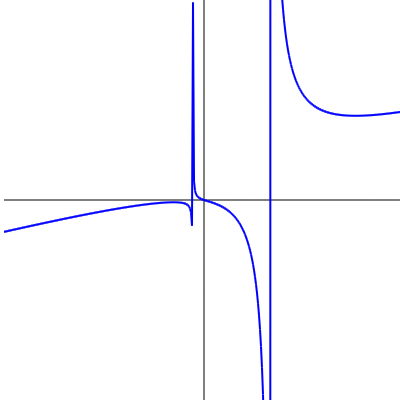


Javascript Y軸に平行な漸近線を描く Mm参考書



標準 微分と関数のグラフと漸近線 なかけんの数学ノート



三角関数のグラフの問題で 周期は求められたんですけど 漸近線のだし方と Clear
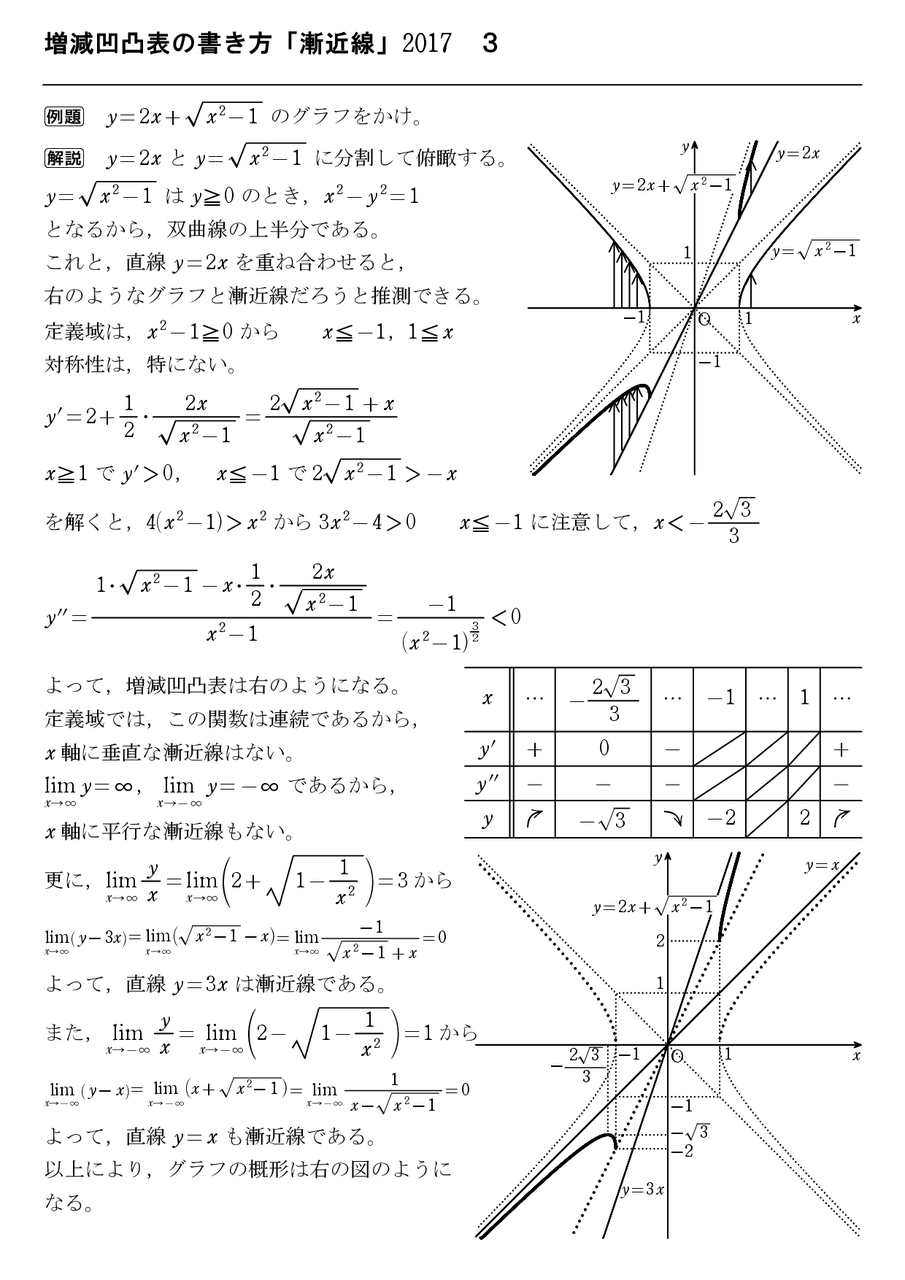


増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する
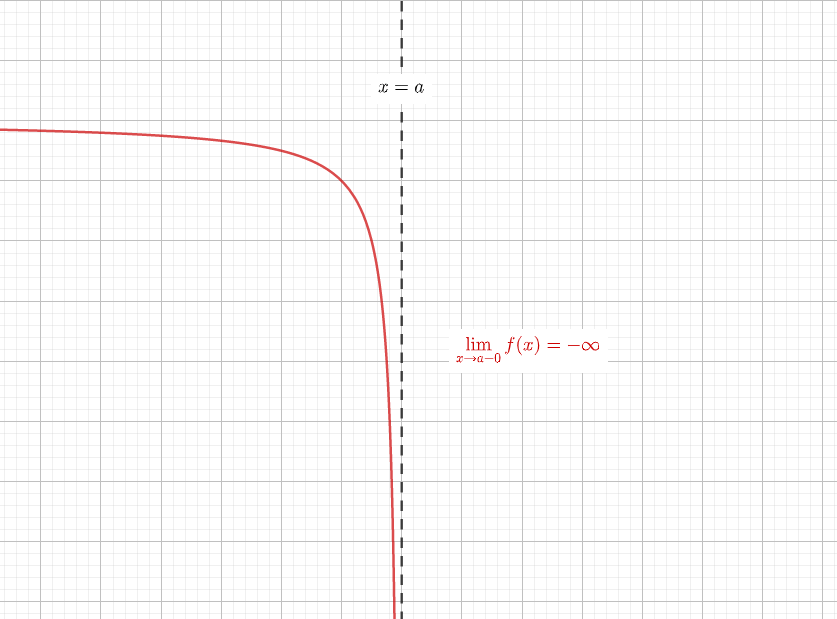


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


双曲線x 2 A 2 Y 2 B 2 1上の点pから2つの漸近 Yahoo 知恵袋



漸近線の求め方 高校数学 微分法の応用 14 Youtube



高校数学 双曲線のグラフ 1 映像授業のtry It トライイット



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



極限のとりかたは理解しているなぜ無限大に極限をとったときと負 高校数学に関する質問 勉強質問サイト



うさぎでもわかる線形代数 第21羽 2次形式の応用 2次曲線のグラフ 工業大学生ももやまのうさぎ塾


漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座



この漸近線の求め方がわかりません なぜy Xをするのか教えて下さい Clear



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube



基本 双曲線と漸近線 なかけんの数学ノート



0 件のコメント:
コメントを投稿